Question

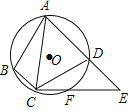
【题目】如图，在中，，经过点A，C且与边AE，CE分别交于点D，F，点B是弧AC上一点，且弧弧BC，连接AB，BC，CD．

求证：≌；

填空：若AC为的直径，则

当的形状为______时，四边形OCFD为菱形；

当的形状为______时，四边形ABCD为正方形．

Answer 1

【答案】等边三角形；等腰直角三角形

【解析】分析：先判断出，进而得出，即可得出结论；
(2) ①先判断出点D是AE的中点，再利用，点F是CE的中点，即可得出，即可得出结论；②先判断出，，进而得出，再判断出，即可得出，即可得出结论．

详解：弧弧BC，
，
是圆内接四边形ABCD的外角，
，
在和中，，
≌；
如图1,①连接AF，

是直径，
，，
四边形OCFD是菱形，
，，
，
，
，
，
，
，
，
，
是等边三角形，
故答案为：等边三角形；
②∵四边形ABCD是正方形，
，，
，
，，
，
，
，
是等腰直角三角形．
故答案为：等腰直角三角形．