Question

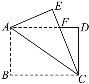
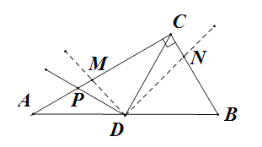
【题目】在Rt△ABC中,∠ACB=90°,∠B=60°.若点D为AB的中点,P为边AB上一点，且∠CDP=90°，将∠CDP绕点D顺时针方向旋转（0°<<60°），角的两边分别与边AC、BC相交于M、N两点，则=_______

Answer 1

【答案】

【解析】

先根据直角三角形斜边上的中线性质得CD=AD=DB，则∠ACD=∠A=30°，∠BCD=∠B=60°，由于∠EDF=90°，可利用互余得∠CPD=60°，再根据旋转的性质得∠PDM=∠CDN=α，于是可判断△PDM∽△CDN，得到，然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=，从而得到解.

∵点D为斜边AB的中点，
∴CD=AD=DB，
∴∠ACD=∠A=30°，∠BCD=∠B=60°，
∵∠EDF=90°，
∴∠CPD=60°，
∴∠MPD=∠NCD，
∵△EDF绕点D顺时针方向旋转α（0°＜α＜60°），
∴∠PDM=∠CDN=α，
∴△PDM∽△CDN，

∴,

在Rt△PCD中，∵tan∠PCD=tan30°=,

∴.

故答案是：.