题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,![]() 、
、![]() 交于点
交于点![]() .
.

(1)直接写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)若![]() ,利用(1)的关系,求出
,利用(1)的关系,求出![]() 的度数;
的度数;
(3)利用(2)的结果,试判断![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,见解析.
,见解析.
【解析】
(1)利用角平分线的定义、三角形的内角和定理即可求出.
(2)直接代入即可求解;
(3)在CB上取点G使得CG=CD,可证△BOE≌△BOG,得BE═BG,可证△CDO≌△CGO,得CD=CG,可以求得BE+CD=BC.
(1)关系是:![]()
理由如下:
∵∠ABC、∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC、∠0CB=
∠ABC、∠0CB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠0CB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (180°∠A)=90°
(180°∠A)=90°![]() ∠A,
∠A,
∴∠BOC=180°(∠OBC+∠0CB)=180°(90°![]() ∠A)=90°+
∠A)=90°+![]() ∠A.
∠A.
即![]()
(2)![]()
(3)答:数量关系是:![]()
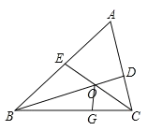
证明:在![]() 上取点
上取点![]() ,使得
,使得![]() ,
,
由(2)知:![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
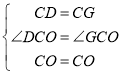
∴![]() ,
,
∴![]() ,
,
∴![]()
又![]() 平分
平分![]()
∴![]()
∴在![]() 和
和![]() 中,
中,

∴![]() ,
,
∴![]()
∵![]()
∴![]() .
.

练习册系列答案
相关题目






