题目内容

设A（x1，y1），B（x2，y2）为函数y=
k2-1x
图象上的两点，且x1＜0＜x2，y1＞y2，则实数k的取值范围是
 
．
分析：先判断出反比例函数图象所在的象限，再根据其增减性解答即可．
解答：解：∵k为常数，函数形式为反比例函数，x1＜0＜x2，y1＞y2，
函数图象只能在二四象限．那么k2-1＜0，k2＜1，
∴-1＜k＜1．
故答案为-1＜k＜1．
点评：可根据所给条件判断反比例函数图象分支所在的象限，进而求解．
练习册系列答案
相关题目
如图，已知C、D是双曲线y=
m
x
在第一象限分支上的两点，直线CD分别交x轴、y轴于A、B两点．设C（x1，精英家教网y1）、D（x2，y2），连接OC、OD（O是坐标有点），若∠BOC=∠AOD=α，且tanα=
1
3
，OC=
10
．
（1）求C、D的坐标和m的值；
（2）双曲线上是否存在一点P，使得△POC和△POD的面积相等？若存在，给出证明，若不存在，说明理由．
设A（ x1，y1）、B （x2，y2）是反比例函数y=-
2
x
图象上的两点．若x1＜x2＜0，则y1与y2之间的关系是（　　）
A、y1＜y2＜0
B、y2＜y1＜0
C、y2＞y1＞0
D、y1＞y2＞0
如图，已知C，D是双曲线y=
m
x
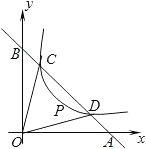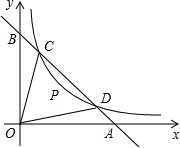（x＞0）上的两点，直线CD分别交x轴，y轴于A，B两点．设C（x1，y1）精英家教网，D（x2，y2），连接OC，OD（O是坐标原点），若∠BOC=∠AOD=α，且tanα=
1
3
，OC=
10
．
（1）求C，D的坐标和m的值；
（2）双曲线存在一点P，使得△POC和△POD的面积相等，求点P的坐标；
（3）在（2）的条件下判断点P是否为△OCD的重心．
（4）已知点Q（-2，0），问在直线AC上是否存在一点M使△MOQ的周长L取得最短？若存在，求出L的最小值并证明；若不存在，请说明理由．
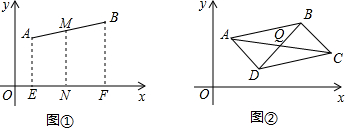让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
1
1
． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
x1+x2
2
x1+x2
2
，
y1+y2
2
y1+y2
2
 ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
x1+x3
2
x1+x3
2
，
y1+y3
2
y1+y3
2
），也可以表示为Q（
x2+x4
2
x2+x4
2
，
y2+y4
2
y2+y4
2
 ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
x1+x3=x2+x4
x1+x3=x2+x4
和
y1+y3=y2+y4
y1+y3=y2+y4
． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
和相等
和相等
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网