题目内容
 如图,Rt△AOB中,O为坐标原点,∠AOB=90°,OA:OB=1:2,如果点A在反比例函数y=
如图,Rt△AOB中,O为坐标原点,∠AOB=90°,OA:OB=1:2,如果点A在反比例函数y=| 1 |
| x |
y=-
| 4 |
| x |
y=-
(填函数解析式)的图象上运动.| 4 |
| x |
分析:如图分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b),则ab=1.根据两角对应相等的两三角形相似,得出△OAC∽△BOD,由相似三角形的对应边成比例,则BD、OD都可用含a、b的代数式表示,从而求出BD•OD的积,进而得出结果.
解答:解:分别过A、B作AC⊥y轴于C,BD⊥y轴于D,设A(a,b),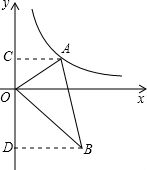
∵点A在反比例函数y=
(x>0)的图象上,
∴ab=1.
在△OAC与△BOD中,∠AOC=90°-∠BOD=∠OBD,∠OCA=∠BDO=90°,
∴△OAC∽△BOD,
∴
=
=
=
,
即
=
=
,
∴BD=2b,OD=2a,
∴BD•OD=4ab=4,
又∵点B在第四象限,
∴点B在函数的图象y=-
上运动.
故答案为:y=-
.

∵点A在反比例函数y=
| 1 |
| x |
∴ab=1.
在△OAC与△BOD中,∠AOC=90°-∠BOD=∠OBD,∠OCA=∠BDO=90°,
∴△OAC∽△BOD,
∴
| OC |
| BD |
| AC |
| OD |
| OA |
| OB |
| 1 |
| 2 |
即
| b |
| BD |
| a |
| OD |
| 1 |
| 2 |
∴BD=2b,OD=2a,
∴BD•OD=4ab=4,
又∵点B在第四象限,
∴点B在函数的图象y=-
| 4 |
| x |
故答案为:y=-
| 4 |
| x |
点评:本题考查了反比例函数的综合题,涉及了相似三角形的判定及性质,用待定系数法求函数的解析式,综合性较强,同学们注意培养自己解答综合题的能力.

练习册系列答案
相关题目
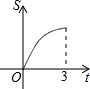
 如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )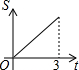


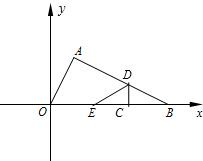 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程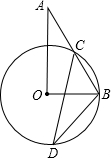 如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数. 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=-