Question

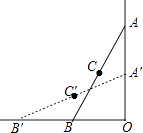
【题目】如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（8，4），将矩形OABC绕点O逆时针旋转，使点B落在y轴上的点B′处，得到矩形OA′B′C′，OA′与BC相交于点D，则经过点D的反比例函数解析式是 ．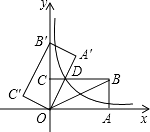

Answer 1

【答案】y=
【解析】解：∵B（8，4）， ∴OA=8，AB=OC=4，
∴A′O=OA=8，A′B′=AB=4，
tan∠COD= = ，
即 = ，
解得CD=2，
∴点D的坐标为（2，4），
设经过点D的反比例函数解析式为y= （k≠0），
则 =4，
解得k=8，
所以，经过点D的反比例函数解析式为y= ．
故答案为：y= ．
利用∠COD的正切值列式求出CD的长度，然后写出点D的坐标，再利用待定系数法求反比例函数解析式解答即可．