题目内容
使得函数值为零的自变量的值称为函数的零点。例如,对于函y=x-1数,令y=0,可得x=1,我们就说1是函数y=x-1的零点。
己知函数y=x2-2mx-2(m+3)(m为常数)。
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且 ,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数解析式。
,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数解析式。
己知函数y=x2-2mx-2(m+3)(m为常数)。
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且
 ,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数解析式。
,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数解析式。 解:(1)当m=0时,该函数为 ,令y=0,可得
,令y=0,可得 ,
,
∴当m=0时,求该函数的零点为 和-
和- ;
;
(2)令y=0,得△= ,
,
∴无论m取何值,方程 总有两个不相等的实数根,即无论m取何值,该函数总有两个零点;
总有两个不相等的实数根,即无论m取何值,该函数总有两个零点;
(3)依题意有 ,
, ,
,
由 得
得 ,即
,即 ,解得
,解得 ,
,
∴函数的解析式为 ,
,
令y=0,解得 ,
,
∵点A在点B左侧,
∴A(-2,0),B(4,0),
作点B关于直线y=x-10的对称点B′,连结AB′,则AB′与直线y=x-10足条件的M点,
易求得直线y=x-10与x轴、y轴点分别为C(10,0),D(0,10),
连结CB′,则∠BCD=45°,
∴BC=CB′=6,∠B′CD=∠BCD=45°,
∴∠BCB′=90°,
即B′(10,-6),
设直线AB′的解析式为 ,
,
则 ,
,
解得
∴直线AB′的解析式为 ,即AM的解析式为
,即AM的解析式为 。
。

 ,令y=0,可得
,令y=0,可得 ,
, ∴当m=0时,求该函数的零点为
 和-
和- ;
;(2)令y=0,得△=
 ,
, ∴无论m取何值,方程
 总有两个不相等的实数根,即无论m取何值,该函数总有两个零点;
总有两个不相等的实数根,即无论m取何值,该函数总有两个零点;(3)依题意有
 ,
, ,
,由
 得
得 ,即
,即 ,解得
,解得 ,
,∴函数的解析式为
 ,
,令y=0,解得
 ,
,∵点A在点B左侧,
∴A(-2,0),B(4,0),
作点B关于直线y=x-10的对称点B′,连结AB′,则AB′与直线y=x-10足条件的M点,
易求得直线y=x-10与x轴、y轴点分别为C(10,0),D(0,10),
连结CB′,则∠BCD=45°,
∴BC=CB′=6,∠B′CD=∠BCD=45°,
∴∠BCB′=90°,
即B′(10,-6),
设直线AB′的解析式为
 ,
,则
 ,
,解得

∴直线AB′的解析式为
 ,即AM的解析式为
,即AM的解析式为 。
。 

练习册系列答案
相关题目
 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 (m为常数).
(m为常数). 和
和 ,且
,且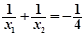 ,此时函数图象与
,此时函数图象与 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式.
上,当MA+MB最小时,求直线AM的函数解析式. ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 (
( m为常数)。
m为常数)。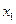 和
和 ,且
,且 ,此时函数图象与x轴的交点分
,此时函数图象与x轴的交点分 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 (k为常数).当k=2时,求该函数的零点;
(k为常数).当k=2时,求该函数的零点;