题目内容
若|m-3|+(n+2)2=0,则m+2n的值为( )
A.-4 B.-1 C.0 D.4
B.
【解析】
试题分析:∵|m-3|+(n+2)2=0,
∴m-3=0且n+2=0,
∴m=3,n=-2.
则m+2n=3+2×(-2)=-1.
故选B.
考点:1.偶次方;2.绝对值.
考点分析: 考点1:有理数 1、有理数的概念:正数和分数统称为有理数.2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 B.
B.
 D.
D.
 的方程
的方程 有实数根,则a的取值范围是 .
有实数根,则a的取值范围是 .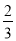 、9、
、9、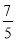 、-(-8)、0、-|+3|,负有理数有( )
、-(-8)、0、-|+3|,负有理数有( ) ,
, ,+(+2),在数轴上表示出来,并用“>”把他们连接起来.
,+(+2),在数轴上表示出来,并用“>”把他们连接起来.