题目内容
两个相似三角形对应中线的比是| 3 |
分析:已知了两相似三角形的对应中线比,即相似比;根据相似三角形的面积比等于相似比的平方,可得出两个相似三角形的面积
比为3:1;由于已知的三角形的面积没有指明是较大三角形的面积,还是较小三角形的面积,因此本题要分类讨论.
比为3:1;由于已知的三角形的面积没有指明是较大三角形的面积,还是较小三角形的面积,因此本题要分类讨论.
解答:解:∵两个相似三角形对应中线的比是
:1,
∴它们的相似比为
:1,
∴它们的面积比为3:1,
①当较小三角形的面积为9时,较大三角形的面积为9×3=27;
②当较大三角形的面积为9时,较小三角形的面积为9÷3=3.
因此另一个三角形的面积为3或27.
| 3 |
∴它们的相似比为
| 3 |
∴它们的面积比为3:1,
①当较小三角形的面积为9时,较大三角形的面积为9×3=27;
②当较大三角形的面积为9时,较小三角形的面积为9÷3=3.
因此另一个三角形的面积为3或27.
点评:本题考查对相似三角形性质的理解,相似三角形面积的比等于相似比的平方.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目



 ,则
,则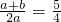 ;⑤一元二次方程x2-x=4的一次项系数是-1;⑥
;⑤一元二次方程x2-x=4的一次项系数是-1;⑥ 不是同类二次根式”中,正确的个数有_____个
不是同类二次根式”中,正确的个数有_____个 ,则
,则 ;⑤一元二次方程x2-x=4的一次项系数是-1;⑥
;⑤一元二次方程x2-x=4的一次项系数是-1;⑥ 不是同类二次根式”中,正确的个数有( )个
不是同类二次根式”中,正确的个数有( )个