题目内容
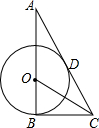 如图,⊙O的半径为3,C是⊙O外一点,且OC=6,过点C作⊙O的两条切线CB,CD.切点分别为B,D,连接BO并延长交切线CD于点A.
如图,⊙O的半径为3,C是⊙O外一点,且OC=6,过点C作⊙O的两条切线CB,CD.切点分别为B,D,连接BO并延长交切线CD于点A.(1)求AD的长;
(2)若M是⊙O上一动点,求CM长的最大值,并说明理由.
考点:切线的性质,含30度角的直角三角形,勾股定理
专题:
分析:(1)连接OD,根据切线的性质,判断△AOD,△ABC为直角三角形,再根据直角三角形的性质以及勾股定理进行解答;
(2)延长CO交⊙O于点M,点M即为所要求的最大值的点,再求其长度即可.
(2)延长CO交⊙O于点M,点M即为所要求的最大值的点,再求其长度即可.
解答:解:(1)连接OD,
∵CD是⊙O的切线
∴OD⊥AC
∵OD=3,OC=6
∴OD=
OC
∴∠OCD=30°
∵CD,CB是⊙O的切线
∴∠ACB=2∠OCD=60°
∴∠A=30°
∴OA=2OD=6,
在Rt△AOD中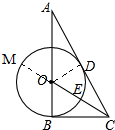
AD=
=
=3
;
(2)延长CO交⊙O于点M,所以点M即为所要求的最大值的点
∵⊙O的半径为3,所以EM=6,
∵OC=6,
∴CE=3
∴CM=CE+EM=3+6=9.
∵CD是⊙O的切线
∴OD⊥AC
∵OD=3,OC=6
∴OD=
| 1 |
| 2 |
∴∠OCD=30°
∵CD,CB是⊙O的切线
∴∠ACB=2∠OCD=60°
∴∠A=30°
∴OA=2OD=6,
在Rt△AOD中

AD=
| OA2-OD2 |
| 62-32 |
| 3 |
(2)延长CO交⊙O于点M,所以点M即为所要求的最大值的点
∵⊙O的半径为3,所以EM=6,
∵OC=6,
∴CE=3
∴CM=CE+EM=3+6=9.
点评:本题考查切线的性质和判定、勾股定理、直角三角形的性质,解题的关键是作出辅助线,找出线段之间的关系进行解答.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下列方程组中是二元一次方程组的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如果
=
,那么
的值为( )
| x+y |
| 3x |
| 1 |
| 2 |
| y |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列为中心对称图形的有( )个
①等腰梯形;②正方形;③平行四边形.
①等腰梯形;②正方形;③平行四边形.
| A、0 | B、1 | C、2 | D、3 |
设⊙O1和⊙O2的半径分别是r1,r2,且r1,r2是关于x的方程x2+ax+1=0的两个根.若⊙O1和⊙O2是等圆,则a的值是( )
| A、a>2或a<-2 | B、a=±2 |
| C、a=2 | D、a=-2 |
 如图,点D、E、F分别在AB,AC,BC上.
如图,点D、E、F分别在AB,AC,BC上. 如图,张雨同学想出了一个测量池塘两端A、B长度的方法:过点A、B引两条直线AC、BC相交于点C,在BC上取点E、G,使BE=CG,再别分别过点E、G作EF∥AB、GH∥AB交AC于点F、H,测得EF=11m,GH=5m,她就得出了结论:池塘的宽AB为16m,你认为她说的对吗?请说明理由.
如图,张雨同学想出了一个测量池塘两端A、B长度的方法:过点A、B引两条直线AC、BC相交于点C,在BC上取点E、G,使BE=CG,再别分别过点E、G作EF∥AB、GH∥AB交AC于点F、H,测得EF=11m,GH=5m,她就得出了结论:池塘的宽AB为16m,你认为她说的对吗?请说明理由.