Question

已知△ABC为锐角三角形，∠C=45°，AD、BE是△ABC的两条高，连接DE，若DE=2，则AB=________．

Answer 1

2
分析：由于AD、BE是△ABC的两条高，可知∠ADC=∠BEC=90°，再加上一组公共角∠C，易证△ADC∽△BEC，那么CD：CE=AC：BC，再结合∠C=∠C，可证△CDE∽△CAB，于是DE：AB=CD：AC，结合cos45°的函数值，可求AB．
解答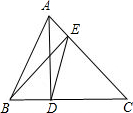：解：如右图所示，
∵AD、BE是△ABC的两条高，
∴∠ADC=∠BEC=90°，
又∵∠C=45°，
∴△ADC∽△BEC，
∴CD：CE=AC：BC，
又∵∠C=∠C，
∴△CDE∽△CAB，
∴DE：AB=CD：AC，
在Rt△ACD中，∠ADC=90°，∠C=45°，
∴cos45°=CD：AC=1：，
∴DE：AB=1：，
∴AB=2．
点评：本题考查了相似三角形的判定和性质、特殊三角函数值．注意两个三角形的两组对应边成比例，且夹角相等，则两三角形相似．