题目内容
把等边△ABC沿直线l对折,使点B落在AC上得P处,AP﹕PC=1﹕2,则BE﹕BF等于( )

| A.1:2 | B.2:3 | C.3:4 | D.4:5 |

如图,
设AP=a,BE=x,BF=y,则PC=2a,AC=3a,
∵△ABC为等边三角形,
∴AB=BC=AC=3a,∠ABC=∠C=∠A=60°,
∴AE=3a-x,CF=3a-y,
∵等边△ABC沿直线l对折,使点B落在AC上得P处,
∴PE=BE=x,PF=BF=y,∠EPF=60°,
∴∠1+∠2=120°,
∵∠1+∠3=120°,
∴∠2=∠3,
∴△AEP∽△CPF,
∴
=
=
,即
=
=
,
∴3ay-xy=2ax①,ay=3ax-xy②,
①+②得4ay=5ax,
∴x:y=4:5,
即BE﹕BF=4:5.
故选D.
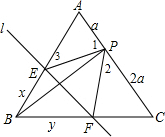
设AP=a,BE=x,BF=y,则PC=2a,AC=3a,
∵△ABC为等边三角形,
∴AB=BC=AC=3a,∠ABC=∠C=∠A=60°,
∴AE=3a-x,CF=3a-y,
∵等边△ABC沿直线l对折,使点B落在AC上得P处,
∴PE=BE=x,PF=BF=y,∠EPF=60°,
∴∠1+∠2=120°,
∵∠1+∠3=120°,
∴∠2=∠3,
∴△AEP∽△CPF,
∴
| AE |
| PC |
| AP |
| FC |
| PE |
| PF |
| 3a-x |
| 2a |
| a |
| 3a-y |
| x |
| y |
∴3ay-xy=2ax①,ay=3ax-xy②,
①+②得4ay=5ax,
∴x:y=4:5,
即BE﹕BF=4:5.
故选D.


练习册系列答案
相关题目