题目内容
如图,y轴的负半轴平分∠AOB,P为y轴负半轴上的一动点,过点P作x轴的平行线分别交OA、OB于点M、N.
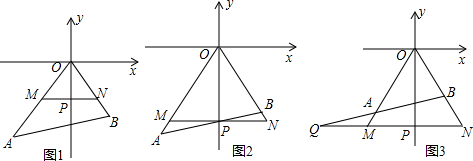
(1)如图1,MN⊥y轴吗?为什么?
(2)如图2,当点P在y轴的负半轴上运动到AB与y轴的交点处,其他条件都不变时,等式∠APM=
(∠OBA-∠A)是否成立?为什么?
(3)当点P在y轴的负半轴上运动到图3处(Q为BA、NM的延长线的交点),其他条件都不变时,试问∠Q、∠OAB、∠OBA之间是否存在某种数量关系?若存在,请写出其关系式,并加以证明;若不存在,请说明理由.

(1)如图1,MN⊥y轴吗?为什么?
(2)如图2,当点P在y轴的负半轴上运动到AB与y轴的交点处,其他条件都不变时,等式∠APM=
| 1 | 2 |
(3)当点P在y轴的负半轴上运动到图3处(Q为BA、NM的延长线的交点),其他条件都不变时,试问∠Q、∠OAB、∠OBA之间是否存在某种数量关系?若存在,请写出其关系式,并加以证明;若不存在,请说明理由.
分析:(1)利用MN∥x轴即可回答.
(2)利用∠OMP=∠N,再结合三角形的外角性质即可证明.
(3)利用∠AMN=∠N,再利用∠AMN=∠Q+∠MAQ和∠OAB=∠MAQ即可证明.
(2)利用∠OMP=∠N,再结合三角形的外角性质即可证明.
(3)利用∠AMN=∠N,再利用∠AMN=∠Q+∠MAQ和∠OAB=∠MAQ即可证明.
解答:解:(1)MN⊥y轴
∵MN∥x轴,
又∵∠XOP=90°,
∴∠OPN=90°,
即MN⊥y轴;
(2)∵PO平分∠AOB,
∴∠AOP=∠BOP,
又∵∠MPO=∠NPO=90°
∴∠OMP=∠N.
∵∠OMP=∠A+∠APM∠APM=∠BPN,
∴∠OBA=∠BPN+∠N=∠APM+∠OMP=∠APM+(∠A+∠APM ).
∴∠APM=
(∠OBA-∠A);
(3)∠Q=
(∠OBA-∠OAB)
∵∠OAB=∠MAQ
∴∠AMN=∠Q+∠MAQ=∠Q+∠OAB
又∵∠AMN=∠N
∴∠N=∠Q+∠OAB
∴∠OBA=∠Q+∠N=∠Q+(∠Q+∠OAB)
即∠Q=
(∠OBA-∠OAB).
∵MN∥x轴,
又∵∠XOP=90°,
∴∠OPN=90°,
即MN⊥y轴;
(2)∵PO平分∠AOB,
∴∠AOP=∠BOP,
又∵∠MPO=∠NPO=90°
∴∠OMP=∠N.
∵∠OMP=∠A+∠APM∠APM=∠BPN,
∴∠OBA=∠BPN+∠N=∠APM+∠OMP=∠APM+(∠A+∠APM ).
∴∠APM=
| 1 |
| 2 |
(3)∠Q=
| 1 |
| 2 |
∵∠OAB=∠MAQ
∴∠AMN=∠Q+∠MAQ=∠Q+∠OAB
又∵∠AMN=∠N
∴∠N=∠Q+∠OAB
∴∠OBA=∠Q+∠N=∠Q+(∠Q+∠OAB)
即∠Q=
| 1 |
| 2 |
点评:考查了三角形内角和定理,平行线的性质和三角形的外角性质,正确的利用∠OMN=∠ONM及三角形的外角性质是解答本题的关键.

练习册系列答案
相关题目
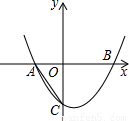
 推理运算:
推理运算: ,CO=BO,AB=3.
,CO=BO,AB=3.
 ,CO=BO,AB=3,则这条抛物线的函数解析式是 .
,CO=BO,AB=3,则这条抛物线的函数解析式是 .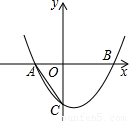
 ,CO=BO,AB=3,则这条抛物线的函数解析式是 .
,CO=BO,AB=3,则这条抛物线的函数解析式是 .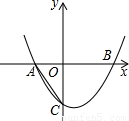
 ,CO=BO,AB=3,则这条抛物线的函数解析式是 .
,CO=BO,AB=3,则这条抛物线的函数解析式是 .