题目内容
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下:
(1)若记销售单价比每瓶进价多x元时,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
| 售价单价(元) | 6 | 7 | 8 | 9 | 11 | 12 |
| 日均销售量(瓶) | 480 | 440 | 400 | 360 | 320 | 240 |
(2)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
分析:(1)若设定价在进价的基础上增加x元,日销售利润为y元,则日均销售量P=480-40(x-1)=520-40x,进而求出y关于x的函数解析式.
(2)利用y=(520-40x)x-200=-40x2+520x-200 (0<x<13)整理函数y,可得x取何值时,y有最大值,即获得最大利润.
(2)利用y=(520-40x)x-200=-40x2+520x-200 (0<x<13)整理函数y,可得x取何值时,y有最大值,即获得最大利润.
解答:解:(1)销售单价每增加1元,日均销售量减少40桶.设在进价基础上增加x元后,日均销售利润为y元,
这时日均销售量P=480-40(x-1)=520-40x,
故y关于x的函数解析式为:y=x(520-40x )-200=-40x2+520x-200(0<x<13),
(2)y=-40x2+520x-200
=-40(x-
)2+1490,
∵0<
<13,
∴当x=
时,即销售单价定为11.5元,日均毛利润达到最大值1490元.
这时日均销售量P=480-40(x-1)=520-40x,
故y关于x的函数解析式为:y=x(520-40x )-200=-40x2+520x-200(0<x<13),
(2)y=-40x2+520x-200
=-40(x-
| 13 |
| 2 |
∵0<
| 13 |
| 2 |
∴当x=
| 13 |
| 2 |
点评:此题考查了二次函数模型的应用,二次函数求最值时,通常考虑对称轴是否在定义域内,对称轴对应的函数值是最值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
(1)若记销售单价比每瓶进价多x元,则销售量为 (用含x的代数式表示);
求日均毛利润(毛利润=售价-进价-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
| 销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
| 日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
求日均毛利润(毛利润=售价-进价-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下表:
| 销售单价(元) | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量(瓶) | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
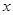 元时,日均毛利润(毛利润=售价
元时,日均毛利润(毛利润=售价 进价
进价 固定成本)为
固定成本)为 元,求
元,求 关于
关于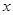 的函数解析式和自变量的取值范围;
的函数解析式和自变量的取值范围;(2)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
(1)若记销售单价比每瓶进价多x元,则销售量为______(用含x的代数式表示);
求日均毛利润(毛利润=售价-进价-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
| 销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
| 日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
求日均毛利润(毛利润=售价-进价-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?