Question

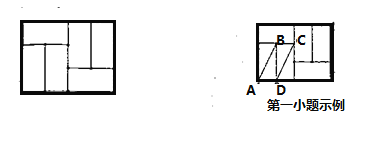
【题目】（1）如图1，四边形中，，点为边的中点，连接并延长交的延长线于点，求证：．（表示面积）

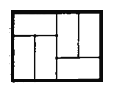
（2）如图2，在中，过边的中点任意作直线，交边于点，交的延长线于点，试比较与的面积，并说明理由．

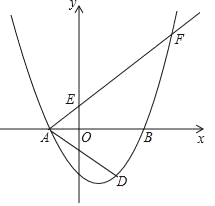
（3）如图3，在平面直角坐标系中，已知一次函数的图像过点且分别于轴正半轴，轴正半轴交于点、，请问的面积是否存在最小值?若存在，求出此时一次函数关系式；若不存在，请说明理由．

Answer 1

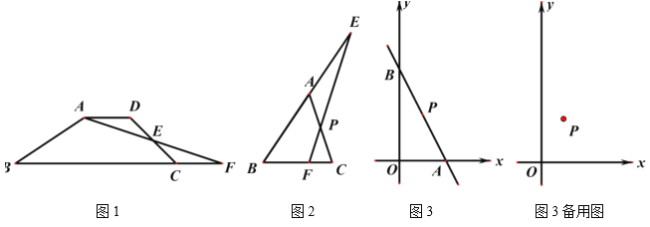
【答案】（1）见解析；（2）S△ABC＜S△EBF，理由见解析；（3）存在，y=-2x+8

【解析】

（1）运用△ADE≌△FCE得出S四边形ABCD=S△ABF；

（2）过A作AM∥BC，交EF与D，证明△PAD≌△PCF，根据全等三角形的性质进行比较即可；

（3）由前两问的结论可得出当点P为AB中点时，△AOB的面积最小，根据直角三角形的性质可得OP=OB=OA，设一次函数表达式为y=kx+b，再综合点P在函数图像上，可得方程，解出即可得到一次函数表达式.

解：（1）∵AD∥BC，
∴∠DAE=∠F，∠D=∠FCE．
∵点E为DC边的中点，
∴DE=CE．
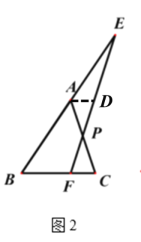
∵在△ADE和△FCE中，

，

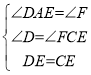∴△ADE≌△FCE（AAS），
∴S△ADE=S△FCE，
∴S四边形ABCE+S△ADE=S四边形ABCE+S△FCE，
即S四边形ABCD=S△ABF；

（2）如图2，过A作AD∥BC，交EF与D，
∵P为AC中点，
∴PA=PC，
∵AD∥BC，
∴∠PAD=∠C
在△PAD和△PCF中，

，

∴△PAD≌△PCF（ASA），
∴S△PAD=S△PCF
∴S△PAD+S△EAD＞S△PCF
即S△PFC＜S△PAE，

则S△ABC＜S△EBF；

（3）由（1）（2）结论可知：当点P为AB中点时，△AOB的面积最小，

连接OP，当△AOB的面积最小时，点P是AB中点，

∴OP=OA=OB，

∵AB过点P（2，4），

设AB表达式为y=kx+b，将点P代入得：b=4-2k，

可得点B坐标为（0，4-2k），

则PB=，

OP==，

∴=，

解得：k=-2或2，

∵AB与x轴、y轴交于正半轴，

∴k≠2，

即k=-2，

此时b=8，

则一次函数的关系式为：y=-2x+8.