题目内容
如图①, 是等边三角形,
是等边三角形, 是顶角
是顶角 的等腰三角形,以
的等腰三角形,以 为顶点作一个
为顶点作一个 角,角两边分别交
角,角两边分别交 边于
边于 两点,连接
两点,连接 .
.
(1)探究:线段 之间的关系,并加以证明。
之间的关系,并加以证明。
(2)若点 是
是 的延长线上的一点,
的延长线上的一点, 是
是 的延长线上的点,其它条件不变,请你再探线段
的延长线上的点,其它条件不变,请你再探线段 之间的关系,在图②中画出图形,直接写出结论.
之间的关系,在图②中画出图形,直接写出结论.
(1)MN=BM+NC.理由如下:
延长AC至E,使得CE=BM(或延长AB至E,使得BE=CN),并连接DE.
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°,
在△MBD与△ECD中,BD=CD,∠MBD=∠ECD,CE=BM,
∴△MBD≌△ECD(SAS),
∴MD=DE,
∴△DMN≌△DEN,
∴MN=BM+NC.
(2)按要求作出图形,(1)中结论不成立,应为MN=NC﹣BM.
在CA上截取CE=BM.
∵△ABC是正三角形,
∴∠ACB=∠ABC=60°,
又∵BD=CD,∠BDC=120°,
∴∠BCD=∠CBD=30°,
∴∠MBD=∠ECD=90°,
又∵CE=BM,BD=CD,
∴△BMD≌△CED(SAS),
∴DE=DM,
又∵ND=ND,∠EDN=∠MDN=60°,MD=ED,
∴△MDN≌△EDN(SAS),
∴MN=NE=NC﹣CE=NC﹣BM.
解析

练习册系列答案
相关题目
 如图,△ABC是等边三角形纸片,沿EF翻折,使点A落在BC边上的D点,设∠AEF=a,AE=x,AF=y.
如图,△ABC是等边三角形纸片,沿EF翻折,使点A落在BC边上的D点,设∠AEF=a,AE=x,AF=y. (2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )
(2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )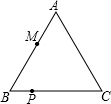 (2013•海淀区一模)如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是( )
(2013•海淀区一模)如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是( ) 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E. 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.
如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.