题目内容
在▱ABCD中,AB<BC,已知∠B=30°,AB=2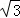 ,将△ABC沿AC翻折至△AB′C,使点B′落在▱ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为
,将△ABC沿AC翻折至△AB′C,使点B′落在▱ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为
4或6 .
解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2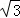 ,
,
∴∠AB′C=30°,
∴GC= B′C=
B′C= BC,
BC,
∴G是BC的中点,
在RT△ABG中,BG= AB=
AB= ×2
×2 =3,
=3,
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2 ,
,
∴BC=AB÷ =2
=2 ×
× =4,
=4,
∴当BC的长为4或6时,△AB′D是直角三角形.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
下列说法正确的是( )
|
| A. | “购买1张彩票就中奖”是不可能事件 |
|
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 |
|
| C. | 了解我国青年人喜欢的电视节目应作全面调查 |
|
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
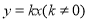 的图象经过点
的图象经过点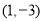 ,则此正比例函数的关系式为( ).
,则此正比例函数的关系式为( ).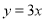 B.
B.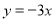 C.
C. D.
D.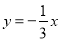
 ,则x2﹣y2的值为
,则x2﹣y2的值为 
 .
.