Question

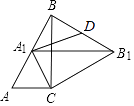
【题目】如图，在△ABC中，∠BAC＝60°，D为AB上一点，连接CD．

(1)如图1，若∠BCA＝90°，CD⊥AB，则＝______(直接写出结果)．

(2)如图2，若BD＝AC，E为CD的中点，AE与BC存在怎样的数量关系，判断并说明理由；

(3)如图3，CD平分∠ACB，BF平分∠ABC，交CD于F．若BF＝AC，求∠ACD的度数．

Answer 1

【答案】(1)；(2)BC＝2AE．理由见解析；(3)∠ACD＝40°．

【解析】

（1）根据含30°的直角三角形即可进行求解；

（2）延长AE至F，使EF＝AE，连接BF，CF，DF，易证△AEC≌△FED，再证△ABF≌△BAC，即可得到BC＝2AE；

（3）在AB上取点G，使AG＝AC，易证△ACG为等边三角形，易证△DGC≌△DFB，得∠DBC＝∠DCB＝∠ACD，即可求出∠ACD＝＝40°．

(1)∵∠BCA＝90°，CD⊥AB，∠BAC＝60°，

∴AD=，AC=

∴AD=

∴＝

(2)BC＝2AE．理由如下：

延长AE至F，使EF＝AE，连接BF，CF，DF，易证△AEC≌△FED，

∴DF＝AC＝BD，∠EAC＝∠EFD，

∴DF∥AC，

∴∠BDF＝∠BAC＝60°，△BDF为等边三角形，

∴∠DBF＝∠BAC＝60°，易证△ABF≌△BAC，

∴AF＝BC，

∴BC＝2AE；

(3)在AB上取点G，使AG＝AC，易证△ACG为等边三角形，

∴GC＝AC＝BF，∠AGC＝60°，

∠BFD＝∠AGC＝60°，易证△DGC≌△DFB，

∴DB＝DC，∴∠DBC＝∠DCB＝∠ACD，

∴∠ACD＝＝40°．