题目内容
（2010•东城区一模）如图，△ABC与△ADE均为等腰直角三角形，∠BAC=∠EAD=90°．求证：△BAE≌△CAD．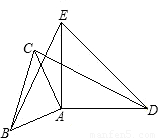
【答案】分析：要证△BAE≌△CAD，由已知可证AB=AC，AE=AD，∠BAC=∠EAD=90°，即可证∠BAE=∠CAD，符合SAS，即得证．
解答：证明：∵△ABC与△AED均为等腰直角三角形，
∴AB=AC，AE=AD，∠BAC=∠EAD=90°（3分）
∴∠BAC+∠CAE=∠EAD+∠CAE．
即∠BAE=∠CAD．（4分）
在△BAE与△CAD中，
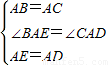
∴△BAE≌△CAD．（5分）
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
解答：证明：∵△ABC与△AED均为等腰直角三角形，
∴AB=AC，AE=AD，∠BAC=∠EAD=90°（3分）
∴∠BAC+∠CAE=∠EAD+∠CAE．
即∠BAE=∠CAD．（4分）
在△BAE与△CAD中，
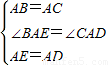
∴△BAE≌△CAD．（5分）
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
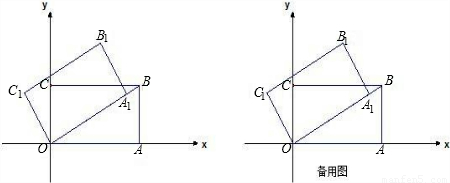
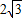，0），B（
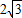，2）．把矩形OABC逆时针旋转30°得到矩形OA1B1C1，
