Question

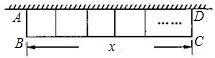
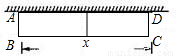
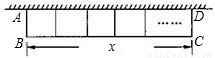
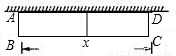
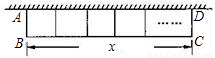
如图，一面利用墙，用篱笆围成的矩形花圃ABCD的面积为S m²，与墙垂直的AB边长为x m．若墙可利用的最大长度为13m，篱笆长为24m，花圃中间用一道篱笆隔成两个小矩形。

(1) 求S与x之间的函数关系式；

（2）当围成的花圃的面积为45m²时，求AB的长；

(3) 当x为何值时，围成的花圃ABCD的面积最大？此时若将矩形花圃ABCD用篱笆隔成n个大小相同的小矩形，使每个小矩形与矩形ABCD相似（原花圃中间的篱笆可移动，且增加的篱笆与墙仍垂直）。则至少还需增加篱笆多少米？

Answer 1

解：（1）………4分

（2）当

整理，得

解得………6分

∴AB的长是3 m。………8分

（3）

………10分

 此时AB=4,BC=12，所隔成的小矩形的长是4 m.

设所隔成的小矩形的宽为a m.

由相似性质得。

  ………11分

4×（9-1-1）=28 m

答：至少还需增加篱笆28米. ………13分