题目内容
4.若关于x的一元二次方程x2+3x-k=0有两个不相等的实数根,则k的取值范围是k>-$\frac{9}{4}$.分析 由方程有两个不相等的实数根即可得出△>0,代入数据即可得出关于k的一元一次不等式,解不等式即可得出结论.
解答 解:∵关于x的一元二次方程x2+3x-k=0有两个不相等的实数根,
∴△=32-4×1×(-k)=9+4k>0,
解得:k>-$\frac{9}{4}$.
故答案为:k>-$\frac{9}{4}$.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是根据根的个数结合根的判别式得出关于k的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出方程(不等式或不等式组)是关键.

练习册系列答案
相关题目
15.用科学记数法表示的数是1.69×105,则原来的数是( )
| A. | 169 | B. | 1690 | C. | 16900 | D. | 169000 |
12. 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
19.-$\frac{1}{3}$的相反数是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
9.不等式组$\left\{\begin{array}{l}{x+3>2}\\{1-2x≤-3}\end{array}\right.$的解集是( )
| A. | x≥2 | B. | -1<x≤2 | C. | x≤2 | D. | -1<x≤1 |
18.下列说法正确的是( )
| A. | “买一张电影票,座位号为偶数”是必然事件 | |
| B. | 若甲、乙两组数据的方差分别为s${\;}_{甲}^{2}$=0.3、s${\;}_{乙}^{2}$=0.1,则甲组数据比乙组数据稳定 | |
| C. | 一组数据2,4,5,5,3,6的众数是5 | |
| D. | 若某抽奖活动的中奖率为$\frac{1}{6}$,则参加6次抽奖一定有1次能中奖 |
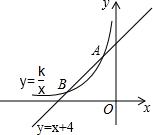 如图,直线y=x+4与双曲线y=$\frac{k}{x}$(k≠0)相交于A(-1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为(0,$\frac{5}{2}$).
如图,直线y=x+4与双曲线y=$\frac{k}{x}$(k≠0)相交于A(-1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为(0,$\frac{5}{2}$).