题目内容
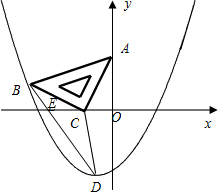
如图,在平面直角坐标系中,将一块腰长为
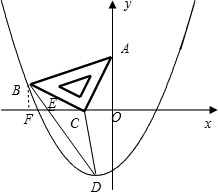
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.
(1)求点A、点B的坐标;
(2)求抛物线的解析式;
(3)设(2)中抛物线的顶点为D,求△DBC的面积.
| 5 |
(1)求点A、点B的坐标;
(2)求抛物线的解析式;
(3)设(2)中抛物线的顶点为D,求△DBC的面积.

∵OC=1,AC=
,
∴OA=
=2,
∴A的坐标为(0,2),
过点B作BF⊥x轴,垂足为F,
则CF=OA=2,BF=OC=1,
∴OF=3,
∴B的坐标为(-3,1);
(2)把B(-3,1)代入y=ax2+ax-2得:
1=9a-3a-2,
a=
,
∴抛物线解析式为y=
x2+
x-2,
(3)如图,可求得抛物线的顶点D(-
,-
).
设直线BD的关系式为y=kx+b(k≠0),将点B、D的坐标代入,求得k=-
,b=-
,
∴BD的关系式为y=-
x-
.
设直线BD和x轴交点为E,则点E(-
,0),CE=
.
∴△DBC的面积为
×
×(1+
)=
.
| 5 |
∴OA=
| AC2-OC2 |
∴A的坐标为(0,2),
过点B作BF⊥x轴,垂足为F,
则CF=OA=2,BF=OC=1,
∴OF=3,
∴B的坐标为(-3,1);
(2)把B(-3,1)代入y=ax2+ax-2得:
1=9a-3a-2,
a=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图,可求得抛物线的顶点D(-
| 1 |
| 2 |
| 17 |
| 8 |
设直线BD的关系式为y=kx+b(k≠0),将点B、D的坐标代入,求得k=-
| 5 |
| 4 |
| 11 |
| 4 |
∴BD的关系式为y=-
| 5 |
| 4 |
| 11 |
| 4 |
设直线BD和x轴交点为E,则点E(-
| 11 |
| 5 |
| 6 |
| 5 |
∴△DBC的面积为
| 1 |
| 2 |
| 6 |
| 5 |
| 17 |
| 8 |
| 15 |
| 8 |


练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
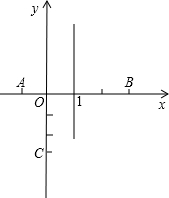
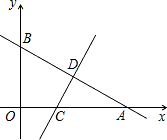 的垂直平分线交x轴于点C,交AB于点D.
的垂直平分线交x轴于点C,交AB于点D.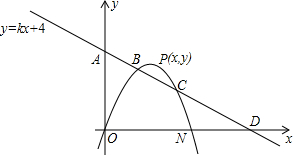 A的面积等于△PON面积的
A的面积等于△PON面积的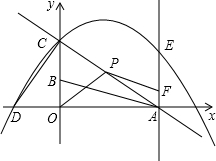 B=
B=