题目内容
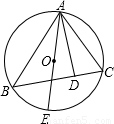
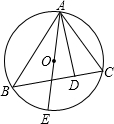 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
(1)求证:∠BAE=∠DAC;
(2)若AB=10,AD=6,CD= ,求⊙O的面积.
,求⊙O的面积.
 解:(1)连接BE,如图,
解:(1)连接BE,如图,∵∠AEB=∠ACD,
而AE是直径
∴∠ABE=90°,
∵AD为△ABC的BC边上的高,
∴∠ADC=∠ABE=90°,
∴∠BAE=∠CAD;
(2)∵AD=6,CD=
 ,
,∴AC=
 =
= ,
,由(1)得△ABE∽△ADC,
∴
 ,
,∴AE=
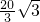 ,
,∴⊙O的半径为
 ,
,∴⊙O的面积为
 .
.分析:(1)连接BE,由AE是直径,得∠ABE=90°,而AD为△ABC的BC边上的高,所以∠ADC=∠ABE=90°,即可得到∠BAE=∠CAD;
(2)先利用勾股定理求出AC=
 =
= ,再利用Rt△ABE∽Rt△ADC,得到
,再利用Rt△ABE∽Rt△ADC,得到 ,即可计算出直径AE,得到圆的半径,可求出⊙O的面积.
,即可计算出直径AE,得到圆的半径,可求出⊙O的面积.点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度.也考查了勾股定理、三角形相似的性质以及圆的面积公式.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
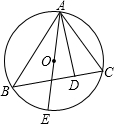 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.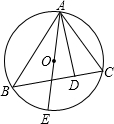

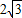 ,求⊙O的面积.
,求⊙O的面积.