Question

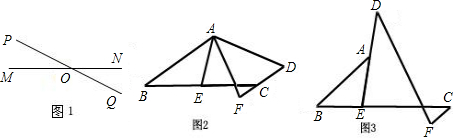
操作：如图①，点O为线段MN的中点，直线PQ与MN相交于点O，请利用图①画出一对以点O为对称中心的全等三角形．
根据上述操作得到的经验完成下列探究活动：
探究一：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的等量关系，并证明你的结论；
探究二：如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC=1：2，∠BAE=∠EDF，CF∥AB．若AB=5，CF=1，求DF的长度．

Answer 1

（1）如图

（2）结论：AB=AF+CF．
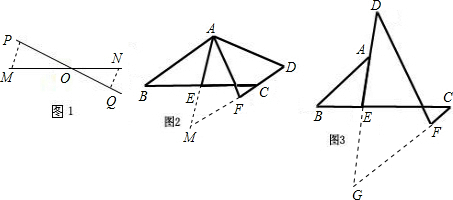
证明：分别延长AE、DF交于点M．
∵E为BC的中点，
∴BE=CE，
∵AB∥CD，
∴∠BAE=∠M，
在△ABE与△MCE中，
∵

∠BAE=∠M ∠AEB=∠MEC BE=CE

，
∴△ABE≌△MCE（AAS），
∴AB=MC，
又∵∠BAE=∠EAF，
∴∠M=∠EAF，
∴MF=AF，
又∵MC=MF+CF，
∴AB=AF+CF；

（3）分别延长DE、CF交于点G．
∵AB∥CF，
∴∠B=∠C，∠BAE=∠G，
∴△ABE∽△GCE，
∴

AB

GC

=

BE

EC

，
又∵

BE

EC

=

1

2

，
∴

AB

GC

=

1

2

，
∵AB=5，
∴GC=10，
∵FC=1，
∴GF=9，
∵AB∥CF，
∴∠BAE=∠G，
又∵∠BAE=∠EDF，
∴∠G=∠EDF，
∴GF=DF，
∴DF=9．