题目内容
(本题满分9分) 如图8,等腰梯形ABCD中,AB∥CD,AD=BC.将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合.
(1)点C是否在以AB为直径的圆上?请说明理由;
(2)当AB=4时,求此梯形的面积.
解:(1)点C在以AB为直径的圆上.
理由:连接MC,MD,
∵AB∥CD,∴∠DCA=∠BAC,
∵∠DAC=∠BAC,∴∠DAC=∠DCA,∴AD=CD,
∵AD=AM,∴CD="AM,"
∴四边形AMCD是平行四边形,∴MC=AD,
同理MD=BC,∵AD=BC,∴MC=MD=AD=BC=MA=MB,
∴点C在以AB为直径的圆上.
(2)由(1)得△AMD是等边三角形,过点D作DE⊥AB于E,
由勾股定理得,DE= ,∴梯形ABCD的面积=
,∴梯形ABCD的面积= .
.
 解析:
解析:
略
理由:连接MC,MD,
∵AB∥CD,∴∠DCA=∠BAC,
∵∠DAC=∠BAC,∴∠DAC=∠DCA,∴AD=CD,
∵AD=AM,∴CD="AM,"
∴四边形AMCD是平行四边形,∴MC=AD,
同理MD=BC,∵AD=BC,∴MC=MD=AD=BC=MA=MB,
∴点C在以AB为直径的圆上.
(2)由(1)得△AMD是等边三角形,过点D作DE⊥AB于E,
由勾股定理得,DE=
 ,∴梯形ABCD的面积=
,∴梯形ABCD的面积= .
. 解析:
解析:略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目


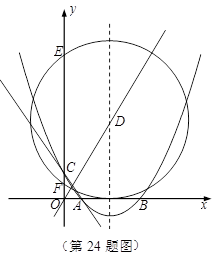
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线
 BD=AC,求∠B︰∠C 的比值
BD=AC,求∠B︰∠C 的比值
 (3)这7天日最高气温的方差是
_______ .
(3)这7天日最高气温的方差是
_______ .