题目内容
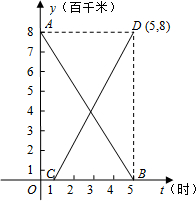 我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开向灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,甲、乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:
我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开向灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,甲、乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?
分析:(1)由图中可明显看出,乙晚甲一小时.通过两地距离及所用时间求出甲乙两机速度;
(2)通过设出函数一般表达式,将坐标代入求出函数关系式;
(3)两函数图象交点的横坐标即为相遇时的时间,将两函数联立求得相遇时间,及相遇时离西宁机场的距离.
(2)通过设出函数一般表达式,将坐标代入求出函数关系式;
(3)两函数图象交点的横坐标即为相遇时的时间,将两函数联立求得相遇时间,及相遇时离西宁机场的距离.
解答:解:(1)由图中可看出,乙机在甲机出发后1小时才从玉树机场出发.甲机飞行速度v1=
÷100=1.6百千米/时,乙机飞行速度
v2=
÷100=2百千米/时
(2)甲机s与t的函数关系式s=-
t+8
乙机s与t的函数关系式s=2(t-1)=2t-2
(3)由图可知:-
t+8=2t-2,
-
t-2t=-2-8,
-(
+2)t=-10,
解得:t=
则乙飞行的时间t-1=
,
乙离开玉树的距离为2×
=
(百千米)=
千米,
离西宁机场的距离s=800-
=
(千米).
| 800 |
| 5 |
v2=
| 800 |
| 4 |
(2)甲机s与t的函数关系式s=-
| 8 |
| 5 |
乙机s与t的函数关系式s=2(t-1)=2t-2
(3)由图可知:-
| 8 |
| 5 |
-
| 8 |
| 5 |
-(
| 8 |
| 5 |
解得:t=
| 25 |
| 9 |
则乙飞行的时间t-1=
| 16 |
| 9 |
乙离开玉树的距离为2×
| 16 |
| 9 |
| 32 |
| 9 |
| 3200 |
| 9 |
离西宁机场的距离s=800-
| 3200 |
| 9 |
| 4000 |
| 9 |
点评:此题为函数图象与实际相结合的问题,同学们应培养运用函数方程解决实际问题的能力.

练习册系列答案
相关题目


