题目内容
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程![]() =0的两个实数根.
=0的两个实数根.
(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=![]() ,求AC、BC的长.
,求AC、BC的长.

【答案】(1)5;(2)AC+BC=![]() CD;(3) AC=6,BC=8或AC=8,BC=6.
CD;(3) AC=6,BC=8或AC=8,BC=6.
【解析】试题分析:(1)根据一元二次方程有两个实数根可得: ![]() ≥0,解得
≥0,解得![]() ≤0,因为
≤0,因为![]() ≥0,所以
≥0,所以![]() =5,
=5,
(2)把(1) ![]() =5代入方程得,
=5代入方程得, ![]() ,所以AD=BD, 将△ADC绕点D逆时针旋转90°后得△BDE,根据圆内接四边形对角互补可得: ∠DAC+∠DBC=180°,所以∠DBE+∠DBC=180°,可证△CDE为等腰直角三角形,所以AC+BC=CE=
,所以AD=BD, 将△ADC绕点D逆时针旋转90°后得△BDE,根据圆内接四边形对角互补可得: ∠DAC+∠DBC=180°,所以∠DBE+∠DBC=180°,可证△CDE为等腰直角三角形,所以AC+BC=CE=![]() CD,
CD,
(3) 由(2)得,AC+BC=![]() CD=
CD=![]()
![]() 7
7![]() =14,由勾股定理可得: AC2+BC2=102=100,
=14,由勾股定理可得: AC2+BC2=102=100,
联立可解得: AC=6,BC=8或AC=8,BC=6.
试题解析:(1)由题意,得 b2-4ac≥0,
∴![]() ≥0,
≥0,
化简整理得, ![]() ≥0,
≥0,
∴![]() ≤0,即
≤0,即![]() ≤0,
≤0,
又∵![]() ≥0,
≥0,
∴![]() =5,
=5,
(2)AC+BC=![]() CD,
CD,
理由是:如图,由(1)得, 当m=5时, ![]() ,
,
∴ AD=BD,
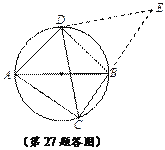
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
将△ADC绕点D逆时针旋转90°后得△BDE,
∴△ADC≌△BDE,
∴∠DAC=∠DBE,
∵∠DAC+∠DBC=180°,
∴∠DBE+∠DBC=180°,
∴点C,B,E三点共线,
∴△CDE为等腰直角三角形,
∴CE=![]() CD,
CD,
即AC+BC=![]() CD,
CD,
(3)由(1)得,当m=5时,b2-4ac![]() ,
,
∴ AD=BD=5![]() ,
,
∵∠ACB=∠ADB=90°,
∴AB=10,
∴AC2+BC2=102=100①,
由(2)得,AC+BC=![]() CD=
CD=![]()
![]() 7
7![]() =14②,
=14②,
由①②解得AC=6,BC=8或AC=8,BC=6.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)判断△BEO的形状,并说明理由.
(2)若AB=5cm,AC=4cm,求△AEF的周长.

【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
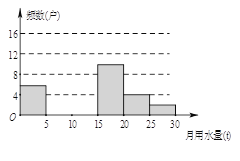
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?




