题目内容
如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE、CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF
B. 点D在∠BAC的平分线上
C. △BDF≌△CDE
D. 点D是BE的中点
D
【解析】由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中, ∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD, 在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL), ∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中, ∠BFD=∠CED=90°, ∠B=∠C, BF=CE,∴△BDF≌△CDE, 选项C正确,而点D不一定是BE的中点,故选D.
试题分析:全等三角形的判定方法有:1.边边边(SSS);2.边角边(SAS);3.角角边(AAS);4.角边角(ASA);5.直角三角形中的斜边直角边(HL);两三角形全等,对应边相等,对应角相等,由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中, ∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD, 在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL), ∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中, ∠BFD=∠CED=90°, ∠B=∠C, BF=CE,∴△BDF≌△CDE, 选项C正确,而点D不一定是BE的中点,故选D.
考点:三角形的全等.

 优加精卷系列答案
优加精卷系列答案 24、如图,AB=AC=AD.
24、如图,AB=AC=AD. (2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.
(2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.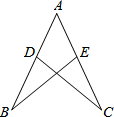 (2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是
(2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是 如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.
如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数. 如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求:
如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求: