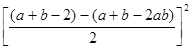题目内容
已知乘法公式：①(a＋b)(a4－a3b＋a2b2－ab3＋b4)＝a5＋b5；②(a－b)(a4＋a3b＋a2b2＋ab3＋b4)＝a5－b5利用上述公式对多项式x8＋x6＋x4＋x2＋1进行因式分解．
答案：
解析：
解析：
|
解：由公式②知： x10－1＝(x2)5－1＝(x2－1)(x8＋x6＋x4＋x2＋1) ∴x8＋x6＋x4＋x2＋1＝ 分析：把待分解的多项式与所给公式比较，会发现待分解的多项式与公式②中的因式a4＋a3b＋a2b2＋ab3＋b4结构相似，事实上，只要令a＝x2，b＝1，则a4＋a3b＋a2b2＋ab3＋b4即x8＋x6＋x4＋x2＋1． 点拨：若本题不能充分利用公式，要想对所给的多项式进行因式分解，很难很难，我们利用了因式分解与多项式的乘法是互为逆变形来解决问题，这也培养了我们的逆向思维能力．本题的创新之处就是利用所给的公式进行因式分解． |
＝
·
＝(x4－x3＋x2－x＋1)(x4＋x3＋x2＋x＋1)
练习册系列答案
相关题目
（2012•随州）在一次数学活动课上，老师出了一道题：
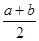+b）2=
)2-(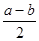
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
+
-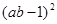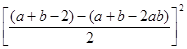