题目内容
17.用适当方法解下列方程:(1)2(x-3)(x+1)=x+1
(2)x2-(1+2$\sqrt{3}$)x+$\sqrt{3}$-3=0.
分析 (1)方程移项后,利用因式分解法求出解即可;
(2)方程利用因式分解法求出解即可.
解答 解:(1)方程移项得:2(x-3)(x+1)-(x+1)=0,
分解因式得:(x+1)(2x-6-1)=0,
解得:x1=-1,x2=3.5;
(2)分解因式得:(x-$\sqrt{3}$)(x-1+$\sqrt{3}$)=0,
解得:x1=$\sqrt{3}$,x2=1-$\sqrt{3}$.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
8.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对某食品质量的调查 | B. | 对数学课本中印刷错误的调查 | ||
| C. | 对学校建立英语角看法的调查 | D. | 对公民保护环境意识的调查 |
5.下列说法不正确的是( )
| A. | 等边三角形有三条对称轴 | |
| B. | 线段AB只有一条对称轴 | |
| C. | 等腰三角形的对称轴是底边上的中线 | |
| D. | 等腰三角形的对称轴是底边上的高所在的直线 |
9.某种品牌的八宝粥,外包装标明:净含量为330±10g,表明了这罐八宝粥的净含量x的范围是( )
| A. | 320<x<340 | B. | 320≤x<340 | C. | 320<x≤340 | D. | 320≤x≤340 |
6.计算-x2•2x3的结果是( )
| A. | -2x5 | B. | 2x5 | C. | -2x6 | D. | 2x6 |
7. 下列图形中,哪个可以通过如图平移得到( )
下列图形中,哪个可以通过如图平移得到( )
 下列图形中,哪个可以通过如图平移得到( )
下列图形中,哪个可以通过如图平移得到( )| A. |  | B. |  | C. |  | D. |  |
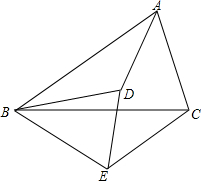 已知,如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,那么△ABD与△BCE相似吗?为什么?
已知,如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,那么△ABD与△BCE相似吗?为什么? 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.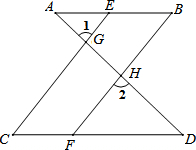 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: