题目内容
.(14分)已知：
是方程
的两个实数根，且
，抛物线
的图像经过点A(
)、B(
).
(1)求这个抛物线的解析式；(3分)
(2)设（1）中抛物线与
轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；(5分)
(3)P是线段OC上的一点，过点P作PH⊥轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标.(6分)
（1）解方程
得
由
，有
所以点A、B的坐标分别为A（1，0）,B（0，5）.
将A（1，0）, B（0，5）的坐标分别代入
.
得
解这个方程组，得
所以，抛物线的解析式为
（2）由，令
，得
解这个方程，得
所以C点的坐标为（-5，0）.由顶点坐标公式计算，得点D（-2，9）.
过D作轴的垂线交轴于M.
则
，
所以，
.
（3）设P点的坐标为（
）
因为线段BC过B、C两点，所以BC所在的值线方程为
.
那么，PH与直线BC的交点坐标为
，
PH与抛物线的交点坐标为
.
由题意，得①
，即
解这个方程，得
或
（舍去）
②
，即
解这个方程，得
或（舍去）
P点的坐标为
或
.
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
与y轴交于点C（0，
）， 与x轴交于点A、 B，点A的坐标为（2，0）．
与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为（
，0）．问：是否存在这样的直线
与
轴交于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程
的两个根.
的周长最小，若存在，请求出点P的坐标；若不存在，请说明理由.
面积S最大时，求m的值.
与
轴交于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程
的两个根.
的周长最小，若存在，请求出点P的坐标；若不存在，请说明理由.
面积S最大时，求m的值.
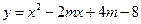
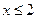时，函数值
随
的增大而减小，求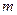
的取值范围。
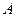为一个顶点作该抛物线的内接正三角形
（
，
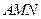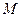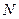两点在抛物线上），请问：△
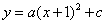与y轴交于点C（0，
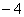）， 与x轴交于点A、 B，点A的坐标为（2，0）．
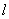与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为（
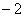，0）．问：是否存在这样的直线