题目内容
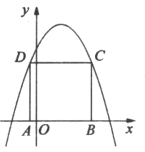
【题目】如图，在平面直角坐标系
中，A、B为x轴上的点，C、D为抛物线y=-x2+2x+3上两点，且四边形ABCD是正方形，则正方形ABCD的面积是__________．
【答案】24-8
【解析】
设正方形的边长为a，令y=a，得a=-x2+2x+3，求解x，则可得出C，D两点的横坐标，再根据CD=a，从而可得出关于a的方程，求出a，即可得出正方形ABCD的面积．
解：设正方形的边长为a，令y=a，得a=-x2+2x+3，
解得x1=1+
，x2=1-，
∴xC=1+，xD=1-，
∴CD=a= xC-xD=1+-1+=2，
∴a2+4a-16=0，
解得a=2-2(舍去负值)，
∴正方形ABCD的面积=a2=24-8．
故答案为：24-8．
练习册系列答案
阅读快车系列答案
相关题目
