题目内容
 如图,在长方形ABCD中,AD=BC=16,AB=DC=12,点P和点Q分别是两个运动的点.动点P从A点出发,沿线段AB,BC向C点运动,速度为每秒2个单位长度;动点Q从B点出发,沿线段BC向C点运动,速度为每秒1个单位长度.P,Q同时出发,从两点出发时开始计时,设运动的时间是t(秒).
如图,在长方形ABCD中,AD=BC=16,AB=DC=12,点P和点Q分别是两个运动的点.动点P从A点出发,沿线段AB,BC向C点运动,速度为每秒2个单位长度;动点Q从B点出发,沿线段BC向C点运动,速度为每秒1个单位长度.P,Q同时出发,从两点出发时开始计时,设运动的时间是t(秒).(1)请用含t的代数式表示下面线段的长度;
当点P在AB上运动时,AP=
2t
2t
;PB=12-2t
12-2t
;当点P运动到BC上时,PB=
2t-12
2t-12
;PC=28-2t
28-2t
.(2)当点P在AB上运动时,t为何值时,线段PB与线段BQ的长度相等?
(3)当t为何值时,动点P与动点Q在BC边上重合?
分析:(1)根据动点P从A点出发,沿线段AB,BC向C点运动,速度为每秒2个单位长度,动点Q从B点出发,沿线段BC向C点运动,速度为每秒1个单位长度,再根据运动的时间是t(秒),即可得出答案.
(2)根据PB=BQ,可得出12-2t=t,再求出t的值即可;
(3)根据动点P在BC上时,BP=BQ,得出2t-12=t,求出t的值即可.
(2)根据PB=BQ,可得出12-2t=t,再求出t的值即可;
(3)根据动点P在BC上时,BP=BQ,得出2t-12=t,求出t的值即可.
解答:解:(1)点P在AB上运动时,AP=2t;
PB=12-2t;
当点P运动到BC上时,PB=2t-12;PC=28-2t;
故答案为:2t,12-2t,2t-12,28-2t.
(2)若PB=BQ,则12-2t=t,
解得t=4,
即t为4秒时,PB=BQ.
(3)当动点P在BC上时,
∵BP=BQ,
∴2t-12=t,
解得t=12,
即t为12秒时,点P与点Q在BC边上重合.
PB=12-2t;
当点P运动到BC上时,PB=2t-12;PC=28-2t;
故答案为:2t,12-2t,2t-12,28-2t.
(2)若PB=BQ,则12-2t=t,
解得t=4,
即t为4秒时,PB=BQ.
(3)当动点P在BC上时,
∵BP=BQ,
∴2t-12=t,
解得t=12,
即t为12秒时,点P与点Q在BC边上重合.
点评:此题考查了一元一次方程的应用,关键是根据图形和已知条件列出方程,注意分两种情况进行讨论.

练习册系列答案
相关题目
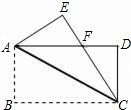 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

