题目内容
如图所示，AD是△ABC的中线，F是AD上一点，CF的延长线交AB于点E，若AF：FD=1：3，则AE：AB=________．
1：7
分析：作DG∥CE，交AB于点G，根据平行推出线段比例关系．
解答：
解：∵AF：FD=1：3
∴
作DG∥CE，交AB于点G
∵D是BC的中点
∴EC=2DG
∴
∴EF=
DG
∴
∴AG=4AE
∴EG=BG=3AE
∴AB=7AE
∴AE：AB=1：7．
点评：本题通过过点D作CE的平行线，把线段的比进行转化．
分析：作DG∥CE，交AB于点G，根据平行推出线段比例关系．
解答：
解：∵AF：FD=1：3∴
作DG∥CE，交AB于点G
∵D是BC的中点
∴EC=2DG
∴
∴EF=
DG∴
∴AG=4AE
∴EG=BG=3AE
∴AB=7AE
∴AE：AB=1：7．
点评：本题通过过点D作CE的平行线，把线段的比进行转化．
练习册系列答案
相关题目
如图所示，AD是△ABC中BC边上的中线，已知△ABC的面积为12，则△ACD的面积等于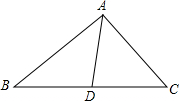
如图所示，AD是△ABC的中线，AB=6cm，AC=5cm，求△ABD和△ADC的周长的差．
55、如图所示，AD是∠BAC的平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，且BD=CD．
26、已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．
如图所示，AD是△ABC的高，AE是⊙O的直径，A，B，C三点都在圆上，∠DAC=30°，则∠BAE为（ ）