Question

【题目】在等边三角形ABC中，AB=6，点D是BC边上的一点，点P是AB边上的一点，连接PD，以PD为边作等边三角形PDE，连接BE．

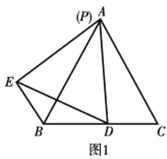
（1）如图1，当点P与点A重合时，

①找出图中的一对全等三角形，并证明；

②BE+BD=；

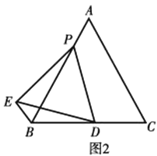
（2）如图2，若AP=1，请计算BE+BD的值．

Answer 1

【答案】（1）①△ACD≌△ABE，证明见解析；②6；（2）BE+BD=5．

【解析】

（1）①根据和均是等边三角形，得到，同时结合角度得和差关系得到，即可得证；

②利用①中证得的可以得到，即可求解；

（2）过点作交于，可以证得是等边三角形，从而根据（1）中的方法证明，即可求解；

（1）当点与点重合时：①，证明如下：

和均是等边三角形

即

在和中：

②：由①得：

（2）过点作交于

是等边三角形,且

，

是等边三角形

,

即

是等边三角形

在和中：

即