题目内容
【题目】定义：对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.
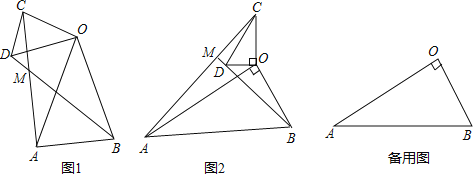
（1）如图①，已知四边形
是⊙
的奇妙四边形，若
，
则
_______；
（2）如图②，已知四边形内接于⊙，对角线交于点
，若
，
①求证：四边形是⊙的奇妙四边形；
②作
于
，请猜想
与
之间的数量关系，并推理说明.
【答案】（1）24；（2）①见解析，②
或
，见解析.
【解析】
(1)由
=S△ADC+S△ABC=
AC·BD即可得到答案.
（2）①证：四边形
是⊙
的奇妙四边形，证
即可.
②过点作
，垂足为点
,
或.
解：（1）
=S△ADC+S△ABC=AC·BD=×6×8=24
（2）如图，由题得，
，
四边形是的⊙奇妙四边形.
②如图，过点作，垂足为点，
与
之间的数量关系：
或
图②
推理说明如下：
解法一：
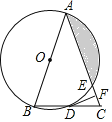
如图③，连结并延长
交⊙于点
，连结
图③
为
的中点
又
为
的中点
是
的中位线
为直径
即
（等角的余角相等）
解法二：
如图③，连结
、
、
、
，过点作
于点，
，
，
，
又
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论：
（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
（2）当﹣
＜x＜2时，y＜0；
（3）a﹣b+c=0；
（4）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧
则其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
