题目内容
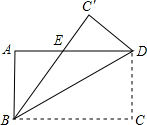
 如图,把长方形ABCD沿BD对折,使C点落在C'的位置时,BC'与AD交于E,若AB=6cm,BC=8cm,求AE的长为
如图,把长方形ABCD沿BD对折,使C点落在C'的位置时,BC'与AD交于E,若AB=6cm,BC=8cm,求AE的长为分析:根据翻折不变性得知∠C′BD=∠CBD,由矩形的性质得AD∥BC,从而得到∠ADB=∠CBD,进而得到ED=EB,设AE的长为x,可知BE的长为(8-x)cm,再根据AB=6cm,在Rt△ABE中,利用勾股定理求出AE的长即可.
解答:解:根据翻折不变性得知∠C′BD=∠CBD,
∵ABCD为矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∴∠C′BD=∠ADB,
∴ED=BE,
∴设AE=xcm,则BE=ED=(8-x)cm,
∴在Rt△ABE中,AB2+AE2=BE2,
∴36+x2=(8-x)2,
36+x2=64+x2-16x,
16x=28,
x=
=
.
故答案为
.
∵ABCD为矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∴∠C′BD=∠ADB,
∴ED=BE,
∴设AE=xcm,则BE=ED=(8-x)cm,
∴在Rt△ABE中,AB2+AE2=BE2,
∴36+x2=(8-x)2,
36+x2=64+x2-16x,
16x=28,
x=
| 28 |
| 16 |
| 7 |
| 4 |
故答案为
| 7 |
| 4 |
点评:此题考查了翻折变换与勾股定理,找到变化中的不变量,将未知量转化到直角三角形中,利用勾股定理解答是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,
, .
. .
. >0.
>0.

 如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.
如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.