题目内容
设A、B在直线l的同侧,已知AB=13,点A、B到直线l的距离分别为10.5和5.5.点C是l上使AC+BC最小的点,则AC+BC=________.
20
分析:以直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称点B′,连接AB′,则线段AB′的长即为AC+BC的最小值,过B作BE⊥y轴于点E,根据勾股定理可求出BE的长,进而可得出A、B′两点的坐标,利用两点间的距离公式即可求解.
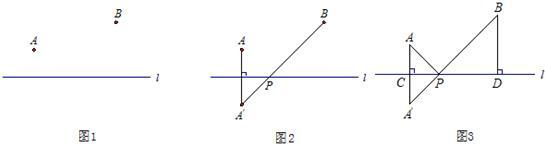
解答: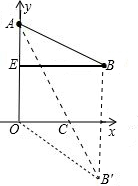 解:如图所示,直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称
解:如图所示,直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称
点B′,连接AB′与x轴相交于点C,由两点之间线段最短可知,线段AB′的长即为AC+BC的最短距离,过B作BE⊥y轴,
∵AB=13,OA=10.5,BD=5.5,
∴AE=OA-BD=10.5-5.5=5,
∴BE=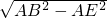 =
=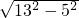 =12,故OD=12,
=12,故OD=12,
∴A、B′两点的坐标分别为(0,10.5)、(12-5.5),
∴AB′=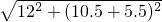 =20.
=20.
故答案为:20.
点评:本题考查的是最短路线问题及两点间的距离公式,解答此题的关键是建立直角坐标系,分别求出A、B′两点的坐标,利用两点间的距离公式求解.
分析:以直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称点B′,连接AB′,则线段AB′的长即为AC+BC的最小值,过B作BE⊥y轴于点E,根据勾股定理可求出BE的长,进而可得出A、B′两点的坐标,利用两点间的距离公式即可求解.
解答:
 解:如图所示,直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称
解:如图所示,直线l为x轴,AC所在的直线为y轴建立直角坐标系,作点B关于x轴的对称点B′,连接AB′与x轴相交于点C,由两点之间线段最短可知,线段AB′的长即为AC+BC的最短距离,过B作BE⊥y轴,
∵AB=13,OA=10.5,BD=5.5,
∴AE=OA-BD=10.5-5.5=5,
∴BE=
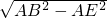 =
=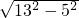 =12,故OD=12,
=12,故OD=12,∴A、B′两点的坐标分别为(0,10.5)、(12-5.5),
∴AB′=
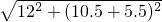 =20.
=20.故答案为:20.
点评:本题考查的是最短路线问题及两点间的距离公式,解答此题的关键是建立直角坐标系,分别求出A、B′两点的坐标,利用两点间的距离公式求解.

练习册系列答案
相关题目
 直线y=-x+m与直线y=
直线y=-x+m与直线y=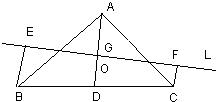

 已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.