题目内容
14.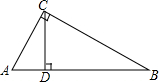 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
分析 由在Rt△ABC中,∠ACB=90°,CD⊥AB,根据同角的余角相等,可得∠ACD=∠B,又由∠CDB=∠ACB=90°,可证得△ACD∽△CBD,然后利用相似三角形的对应边成比例,即可求得答案.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}$=$\frac{CD}{BD}$,
∵AD=2,CD=4,
∴$\frac{2}{4}$=$\frac{4}{BD}$,
∴BD=8.
点评 本题考查了相似三角形的判定与性质以及直角三角形的性质.此题难度不大,解题的关键是掌握有两角对应相等的三角形相似与相似三角形的对应边成比例定理的应用.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | (-3x2y)3=-27x6y3 |
9.下列运算正确的是( )
| A. | -3-2=-1 | B. | -32=8 | C. | 2xy+xy=3xy | D. | 2x+x2=3x3 |
19. 如图,把一个半圆沿着虚线旋转一周得到的图形为( )
如图,把一个半圆沿着虚线旋转一周得到的图形为( )
 如图,把一个半圆沿着虚线旋转一周得到的图形为( )
如图,把一个半圆沿着虚线旋转一周得到的图形为( )| A. |  | B. |  | C. |  | D. |  |
6.4的平方根是( )
| A. | 2 | B. | -2 | C. | 16 | D. | ±2 |
3.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{x-1}{|x|}<0}\\{2x+1>a}\end{array}\right.$有且只有一个整数解,则a的取值范围是( )
| A. | -1<a≤1 | B. | -1≤a<1 | C. | -3<a≤-1 | D. | -3≤a<-1 |
4.下面计算结果正确的是(( )
| A. | b3•b3=2b3 | B. | x4•x4=x16 | C. | (ab2)3=a3b6 | D. | (-2a)2=-4a2 |
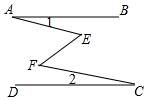 已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.
已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.