题目内容
（2013•泸州）已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为（ ）
分析：先根据题意画出图形，由于点C的位置不能确定，故应分两种情况进行讨论．
解答：
解：连接AC，AO，
∵⊙O的直径CD=10cm，AB⊥CD，AB=8cm，
∴AM=
AB=
×8=4cm，OD=OC=5cm，
当C点位置如图1所示时，
∵OA=5cm，AM=4cm，CD⊥AB，
∴OM=
=
=3cm，
∴CM=OC+OM=5+3=8cm，
∴AC=
=
=4
cm；
当C点位置如图2所示时，同理可得OM=3cm，
∵OC=5cm，
∴MC=5-3=2cm，
在Rt△AMC中，AC=
=
=2
cm．
故选C．
解：连接AC，AO，∵⊙O的直径CD=10cm，AB⊥CD，AB=8cm，
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
当C点位置如图1所示时，
∵OA=5cm，AM=4cm，CD⊥AB，
∴OM=
| OA2-AM2 |
| 52-42 |
∴CM=OC+OM=5+3=8cm，
∴AC=
| AM2+CM2 |
| 42+82 |
| 5 |
当C点位置如图2所示时，同理可得OM=3cm，
∵OC=5cm，
∴MC=5-3=2cm，
在Rt△AMC中，AC=
| AM2+MC2 |
| 42+22 |
| 5 |
故选C．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
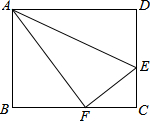（2013•泸州）如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，点D的对称点F恰好落在BC上，已知折痕AE=10
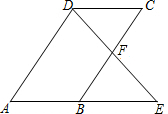（2013•泸州）如图，已知?ABCD中，F是BC边的中点，连接DF并延长，交AB的延长线于点E．求证：AB=BE．
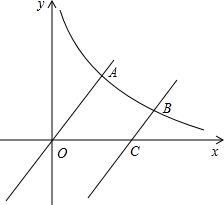（2013•泸州）如图，已知函数y=