题目内容
如图,四边形ABCD是矩形,AB=3,AD=4,直线PS分别交AB、CD的延长线于P、S,交BC、AC、AD于Q、E、R,BP=1,DS=2.
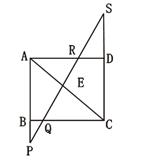
(1)写出图中相似三角形(不含全等三角形);
(2)请找出图中除AB=CD、BC=AD以外的相等线段,并证明你的判断.
(3)求四边形ABQR与四边形CQRD的面积比.

(1)写出图中相似三角形(不含全等三角形);
(2)请找出图中除AB=CD、BC=AD以外的相等线段,并证明你的判断.
(3)求四边形ABQR与四边形CQRD的面积比.
(1)△SRD∽△SQC、△SRD∽△PRA、△SRD∽△PQB、△PBQ∽△SCQ、△PBQ∽△PAR、△ARE∽△CQE、△PEA∽△SEC;(2)AP=AD、AC=SC;(3)5:7.
试题分析:(1)根据相似三角形的判定方法结合图形的特征求解即可;
(2)由AB=3,AD=4,BP=1,DS=2结合勾股定理求解即可;
(3)设BQ=
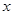 ,则QC=4-
,则QC=4-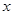 ,由△PBQ∽△SCQ根据相似三角形的性质可求得x,即可求得BQ、QC的长,由△SRD∽△SQC根据相似三角形的性质可求得RD、AR的长,再根据三角形的面积公式求解即可.
,由△PBQ∽△SCQ根据相似三角形的性质可求得x,即可求得BQ、QC的长,由△SRD∽△SQC根据相似三角形的性质可求得RD、AR的长,再根据三角形的面积公式求解即可.(1)△SRD∽△SQC、△SRD∽△PRA、△SRD∽△PQB、△PBQ∽△SCQ、△PBQ∽△PAR、△ARE∽△CQE、△PEA∽△SEC;
(2)∵四边形ABCD是矩形,AB=3,AD=4,BP=1,DS=2
∴AP=AD=4,AC=SC=5;
(3)设BQ=
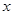 ,则QC=4-
,则QC=4-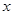
∵△PBQ∽△SCQ
∴
 ,即
,即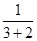 =
=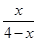 ,解得
,解得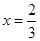
即BQ=
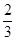 ,QC=
,QC=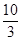
∵△SRD∽△SQC
∴
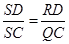 ,RD
,RD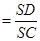 . QC
. QC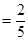 ·
·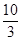
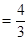 ,AR=4
,AR=4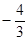
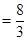
∴S四ABQR=
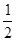 (BQ+AR)·AB
(BQ+AR)·AB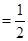 ·(
·(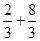 )·3=5
)·3=5 ∴S四RDCQ=S四ABCD-S四ABQR=3×4-5=7
∴S四ABQR:S四CQRD=5:7.
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD. 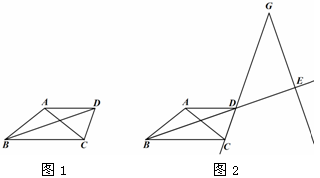
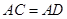 ;
; 为线段
为线段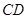 延长线上一点,将射线GC绕着点G逆时针旋转
延长线上一点,将射线GC绕着点G逆时针旋转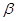 ,与射线BD交于点E.
,与射线BD交于点E. ,
, ,如图2所示,求证:
,如图2所示,求证: ;
; ,
, ,请直接写出
,请直接写出 的值(用含
的值(用含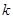 的代数式表示).
的代数式表示).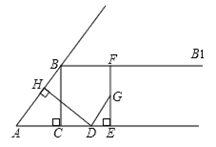
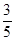 时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?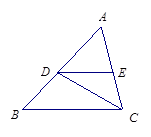
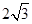 ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G. =
= =
= =
= ,且△ABC的周长为15cm,则△ADE的周长为( )
,且△ABC的周长为15cm,则△ADE的周长为( )