题目内容
【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.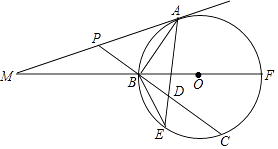
(1)求证: ![]() =
= ![]() ;
;
(2)若ED、EA的长是一元二次方程x2﹣5x+5=0的两根,求BE的长;
(3)若MA=6 ![]() ,sin∠AMF=
,sin∠AMF= ![]() ,求AB的长.
,求AB的长.
【答案】
(1)证明:连接OA、OE交BC于T.
∵AM是切线,
∴∠OAM=90°,
∴∠PAD+∠OAE=90°,
∵PA=PD,
∴∠PAD=∠PDA=∠EDT,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠EDT+∠OEA=90°,
∴∠DTE=90°,
∴OE⊥BC,
∴ ![]() =
= ![]() .
.

(2)∵ED、EA的长是一元二次方程x2﹣5x+5=0的两根,
∴EDEA=5,
∵ ![]() =
= ![]() ,
,
∴∠BAE=∠EBD,∵∠BED=∠AEB,
∴△BED∽△AEB,
∴ ![]() =
= ![]() ,
,
∴BE2=DEEA=5,
∴BE= ![]() .
.
(3)作AH⊥OM于H.
在Rt△AMO中,∵AM=6 ![]() ,sin∠M=
,sin∠M= ![]() =
= ![]() ,设OA=m,OM=3m,
,设OA=m,OM=3m,
∴9m2﹣m2=72,
∴m=3,
∴OA=3,OM=9,
易知∠OAH=∠M,
tan∠OAH=![]() ,
,
∴OH=1,AH=2 ![]() .BH=2,
.BH=2,
∴AB= ![]() =
= ![]()
![]()
![]()
【解析】(1)要证两弧相等,可由垂径定理的推论须证直径垂直于弧所对的弦即可,须连结OE,证OE![]() BC;(2)利用第(1)问的结论
BC;(2)利用第(1)问的结论 ![]() =
= ![]() ,∴∠BAE=∠EBD,可得△BED∽△AEB,由对应边成比例可得BE2=DEEA,再由根与系数的关系得DEEA=5,即BE=
,∴∠BAE=∠EBD,可得△BED∽△AEB,由对应边成比例可得BE2=DEEA,再由根与系数的关系得DEEA=5,即BE= ![]() ;(3)利用三角函数的基本方法是把这个角放到直角三角形中,因此须作AH⊥OM于H,由正弦求出对边=
;(3)利用三角函数的基本方法是把这个角放到直角三角形中,因此须作AH⊥OM于H,由正弦求出对边=![]() ,再转化∠OAH=∠M,由正弦求正切,求出OH,进而算出BH,利用勾股定理算出AB.
,再转化∠OAH=∠M,由正弦求正切,求出OH,进而算出BH,利用勾股定理算出AB.
【考点精析】关于本题考查的根与系数的关系和切线的性质定理,需要了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案