题目内容
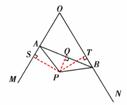
已知,如图①,∠MON=60°,点A、B为射线OM、ON上的动点(点A、B不与点O重合),且AB=![]() ,在∠MON的内部、△AOB的外部有点P,且AP=BP,∠APB=120°.
,在∠MON的内部、△AOB的外部有点P,且AP=BP,∠APB=120°.
(1)求AP的长;
(2)求证:点P在∠MON的平分线上;
(3)如图②,点C,D,E,F分别是四边形AOBP
的边AO,OB,BP,PA的中点,连接CD,DE,EF,
FC,OP. ①当AB⊥OP时,请直接写出四边形CDEF的周长;②若四边形CDEF的周长用t表示,请直接写出t的取值范围.


解:
(1) 过点P作PQ⊥AB于点Q
∵PA=PB,∠APB=120° ,AB=4![]() ,
,
∴AQ=![]() AB=
AB=![]() ×4
×4![]() =2
=2![]() ,∠APQ=
,∠APQ=![]() ∠APB=
∠APB=![]() ×120°=60°
×120°=60°
在Rt△APQ中, sin∠APQ=![]()
∴AP= 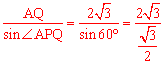 =4
=4
(2)证明:过点P分别作PS⊥OM于点S, PT⊥ON于点T
∴∠OSP=∠OTP=90°
在四边形OSPT中,∠SPT=360°-∠OSP-∠SOT-∠OTP=360°-90°-60°-90°=120°,
 ∴∠APB=∠SPT=120°
∴∠APB=∠SPT=120°
∴∠APS=∠BPT
又∵∠ASP=∠BTP=90°, AP=BP,
∴△APS≌△BPT
∴PS=PT
∴点P在∠MON的平分线上(3) ①8+4![]()
②4+4![]() <t≤8+4
<t≤8+4![]()

练习册系列答案
相关题目
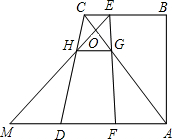 EH交AD的延长线于点M,交AC于点O,设EC=x.
EH交AD的延长线于点M,交AC于点O,设EC=x. 25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N.
25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N. (1998•河北)已知:如图,在⊙O中,直径AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,连接MO并延长,交⊙O于N.则下列结论中,正确的是( )
(1998•河北)已知:如图,在⊙O中,直径AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,连接MO并延长,交⊙O于N.则下列结论中,正确的是( )
 .点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.
.点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.