题目内容
【题目】如图，已知
平分
， 
于
， 
于
，且
．
（
）求证： 
≌
．
（
）若
， 
， 
，求
的长．
【答案】（
）证明见解析；（
）
．
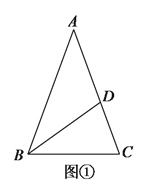
【解析】试题分析：（1）已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，根据角平分线的性质定理可得CE=CF，再由
，根据HL即可判定△BCE≌△DCF；（2）由Rt△BCE≌△Rt△DCF可得DF=EB，再由HL证明Rt△AFC≌△Rt△AEC，即可得AE=AF，设DF=x，则有9+x=21-x，得x=6，在Rt△CDF中，根据勾股定理求得CF=8，在Rt△AFC中，再运用勾股定理求得AC即可．
试题解析：
（
）证明：∵
平分
， 
于
， 
于
，
∴
， 
， 
，
∵
，
∴
≌
．
（
）由（
）得， 
≌
，
∴
，
∵
与
中，
，
∴
≌
，
∴
，
设
，则有
，得
，
在
中， 
， 
，
∴
，
在
中， 
， 
，
∴
．
练习册系列答案
优等生题库系列答案
相关题目
