题目内容
如图,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=![]() .特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.
.特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.

(1)如图,在△ABC中,∠C=90o,∠A=30o,求λA、λC;

(2)在每个小正方形边长均为1的4×4的方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积也为2;
(3)判断下列三个命题的真假(真命题打“√”,假命题打“×”):
①若△ABC中λA<1,则△ABC为锐角三角形;( )
②若△ABC中λA=1,则△ABC为锐角三角形;( )
③若△ABC中λA>1,则△ABC为锐角三角形.( )
答案:
解析:
解析:
|
解:(1)如图,作BC边上的中线AD,又AC⊥BC. ∴λA= 过点C分别作AB边上的高CE和中线CF 1分
∵∠ACB=90o ∴AF=CF ∴∠ACF=∠CAF=30o ∴∠CFE=60o ∴λC= (2) (画出的图形满足=2就给2分) 3分
(3)×;√;√ 3分 (每小题各1分,若出现写“真”“假”或写“对”“错”同样给分) |

练习册系列答案
相关题目


 25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
25、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.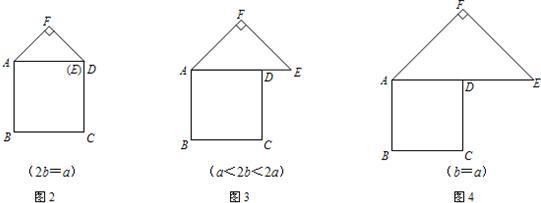


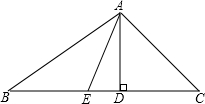 如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数. 如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.