题目内容
【题目】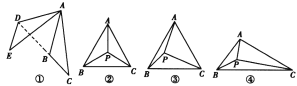
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
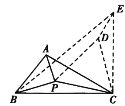
如图③,在边长为![]() 的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
【答案】(1)60,理由见解析;(2)见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)【操作发现】:如图1中,只要证明△DAB是等边三角形即可;
(2)【类比探究】:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.利用全等三角形的性质以及三角形的三边关系即可解决问题;
(3)【解决问题】:如图3中,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;
(4)【拓展应用】:如图4中,先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=4,∠PCD=60°,再证明∠BCE=90°,然后在Rt△BCE中,由勾股定理求出BE的长度,即为PA+PB+PC的最小值;
(1)【操作发现】60.
理由:∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°.
(2)【类比探究】证明:如图,以PA为边长作等边△PAD,使 P,D分别在,AC的两侧,连接CD.
∵∠BAC=∠PAD=60°
∴∠BAP=∠CAD.
∵AB=AC,AP=AD,
∴△PAB≌△DAC(SAS),
∴BP=CD.
在△PCD中,∵PD+CD>PC.
又∵AP=PD,
∴AP+BP>PC.
∴以PA,PB,PC的长为三边必能组成三角形.
(3)【解决问题】如图,将△APB绕点A按逆时针方向旋转60°,得到△AP′C,
∴∠AP′C=∠APB=360°-90°-120°=150°,
AP=AP′,∠PAP′= 60∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=150°-60°=90°, ∠P′PC=∠APC-∠APP′=30°,
∴PP′=![]() ,即AP=
,即AP=![]() .
.
∵∠APC=90°,AC=![]() ,
,
∴AP +PC =AC,即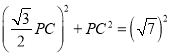 ,
,
∴PC=2(舍负),∴AP=![]() ,∴
,∴![]() .
.
(4)【拓展应用】如图,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD,BE.
∵将△APC绕点C顺时针旋转60°得到△EDC,
∴△APC≌△EDC,∠PCD=60°
∴∠ACP=∠ECD,AC=EC=4,
∴∠ACB=∠ACP+∠PCB=∠ECD+∠PCB=30°,
∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°.
在Rt△BCE中,∵BC=5,CE=4,
∴![]() ,
,
当P,D在BE上时,PA+PB+PC=BE,此时PA+PB+PC取最小值,为![]() .
.

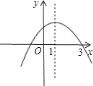
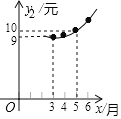
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?