题目内容
解方程与不等式
(1)
(2)
,并求出它的整数解的和.
(1)
|
(2)
|
分析:(1)变形后由①得出x=2y,代入②即可求出y的值,代入x=2y求出x即可.
(2)求出两不等式的解集,求出不等式组的解集,求出不等式组的整数解,相加即可.
(2)求出两不等式的解集,求出不等式组的解集,求出不等式组的整数解,相加即可.
解答:解:(1)方程组化为:
由①得:x=2y③,
把③代入②得:4y+y=10,
解得:y=2,
把y=2代入③得:x=4,
即原方程组的解为:
.
(2)∵解不等式2x+3>3x得:x<3,
解不等式
-
≥
得:x≥-4,
∴不等式组的解集为-4≤x<3,
∴不等式组的整数解是-4,-3,-2,-1,1,2,
∴不等式组的整数解的和为-4-3-2-1+1+2=-7.
|
由①得:x=2y③,
把③代入②得:4y+y=10,
解得:y=2,
把y=2代入③得:x=4,
即原方程组的解为:
|
(2)∵解不等式2x+3>3x得:x<3,
解不等式
| x+3 |
| 3 |
| x-1 |
| 6 |
| 1 |
| 2 |
∴不等式组的解集为-4≤x<3,
∴不等式组的整数解是-4,-3,-2,-1,1,2,
∴不等式组的整数解的和为-4-3-2-1+1+2=-7.
点评:本题考查了解二元一次方程组和解一元一次不等式组的应用,主要考查学生的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
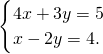
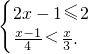 .
. ;
;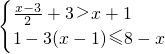 .
. ;
;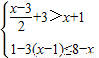 .
.