题目内容
(2009•崇文区一模)已知:关于x的一元二次方程kx2+(2k-3)x+k-3=0有两个不相等实数根(k<0).(1)用含k的式子表示方程的两实数根;
(2)设方程的两实数根分别是x1,x2(其中x1>x2),若一次函数y=(3k-1)x+b与反比例函数y=
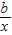 的图象都经过点(x1,kx2),求一次函数与反比例函数的解析式.
的图象都经过点(x1,kx2),求一次函数与反比例函数的解析式.
【答案】分析:根据根的判别式和求根公式,求出x的值.由x1<x2及k<0确定x1与x2的值,再把交点的坐标代入两个函数的解析式,求出k和b的值,从而得出函数的解析式.
解答:解:(1)∵kx2+(2k-3)x+k-3=0是关于x的一元二次方程.
∴△=(2k-3)2-4k(k-3)=9,
由求根公式,得
 .
.
∴x=-1或 .
.
(2)∵k<0,∴ .
.
而x1>x2,∴x1=-1, .
.
由题意得:
解之,得 .
.
∴一次函数的解析式为y=-16x-8,反比例函数的解析式为 .
.
点评:本题考查了根的判别式和用待定系数法.
解答:解:(1)∵kx2+(2k-3)x+k-3=0是关于x的一元二次方程.
∴△=(2k-3)2-4k(k-3)=9,
由求根公式,得
 .
.∴x=-1或
 .
.(2)∵k<0,∴
 .
.而x1>x2,∴x1=-1,
 .
.由题意得:

解之,得
 .
.∴一次函数的解析式为y=-16x-8,反比例函数的解析式为
 .
.点评:本题考查了根的判别式和用待定系数法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 交y轴于D点,E为抛物线顶点.若∠DBC=α,∠CBE=β,求α-β的值.
交y轴于D点,E为抛物线顶点.若∠DBC=α,∠CBE=β,求α-β的值.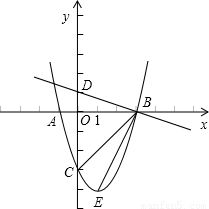
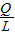 =______;
=______;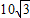 ,且∠ABC=60°,求CD的长.
,且∠ABC=60°,求CD的长.