题目内容
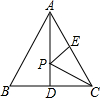如图，点E为等边△ABC中AC边的中点，AD⊥BC，且AD=5，P为AD上的动点，则PE+PC的最小值为5
5
．分析：先根据锐角三角函数的定义求出AB的长，连接BE，则线段BE的长即为PE+PC最小值．
解答：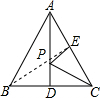
解：∵△ABC是等边三角形，AD⊥BC，且AD=5，
∴AB=
=
=
，
连接BE，线段BE的长即为PE+PC最小值，
∵点E是边AC的中点，
∴CE=
AB=
×
=
cm，
∴BE=
=
=
=5，
∴PE+PC的最小值是5．
故答案为：5．
解：∵△ABC是等边三角形，AD⊥BC，且AD=5，∴AB=
| AD |
| sin60° |
| 5 | ||||
|
10
| ||
| 3 |
连接BE，线段BE的长即为PE+PC最小值，
∵点E是边AC的中点，
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
10
| ||
| 3 |
5
| ||
| 3 |
∴BE=
| BC2-CE2 |
(
|
| 15 |
| 3 |
∴PE+PC的最小值是5．
故答案为：5．
点评：本题考查的是轴对称-最短路线问题，熟知等边三角形的性质是解答此题的关键．
练习册系列答案
相关题目
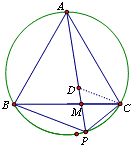
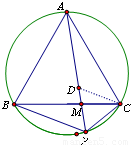
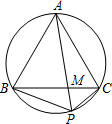如图，点P为等边△ABC外接圆劣弧BC上一点．
如图，点P为等边△ABC的边AB上一点，Q为BC延长线上一点，AP=CQ，PQ交AC于D，
