题目内容
二次函数y=x2-mx+m-2的图象的顶点到x轴的距离为 ,求二次函数解析式.
,求二次函数解析式.
解:∵二次函数y=x2-mx+m-2的图象的顶点到x轴的距离为 ,a=1>0,
,a=1>0,
∴抛物线开口向上,故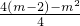 =-
=- ;
;
解得(2m-1)(2m-7)=0,
m1= ,m2=
,m2= ;
;
故函数解析式为y=x2- x-
x- 或y=x2-
或y=x2- x+
x+ .
.
分析:由于函数图象到x轴的距离为 ,则函数的顶点纵坐标为-
,则函数的顶点纵坐标为- 或
或 .
.
点评:本题考查了待定系数法求二次函数解析式,根据顶点到x轴的距离求出m的值是解题的关键.
 ,a=1>0,
,a=1>0,∴抛物线开口向上,故
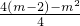 =-
=- ;
;解得(2m-1)(2m-7)=0,
m1=
 ,m2=
,m2= ;
;故函数解析式为y=x2-
 x-
x- 或y=x2-
或y=x2- x+
x+ .
.分析:由于函数图象到x轴的距离为
 ,则函数的顶点纵坐标为-
,则函数的顶点纵坐标为- 或
或 .
.点评:本题考查了待定系数法求二次函数解析式,根据顶点到x轴的距离求出m的值是解题的关键.

练习册系列答案
相关题目